在本文中,我们介绍了一套三件套,以了解货币流通。 三件套是循环流程图、名义GDP的定义、数量方程(Fisher's equation of exchange)。 这些项目在现代经济学中是独立的。 我们整合它们以进行货币流通。 作为结论,我们得到 M=G+I=S+T 和 V=Y/(G+I)。
本文的内容如下。
1. 三件套
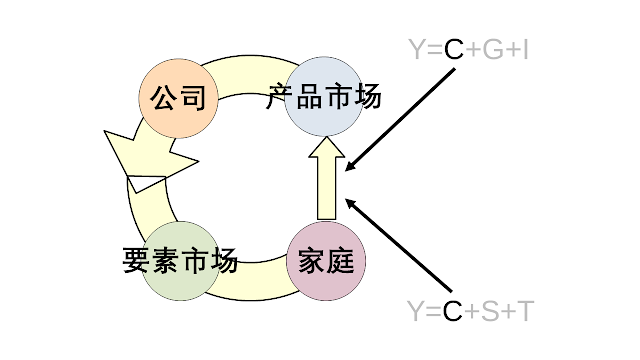
我们的三件套是循环流程图、名义 GDP 的定义和数量方程。 首先,我们介绍循环流程图。 如果您不知道,您可以通过图像搜索找到循环流程图的图像。
该图中的箭头显示了资金的流动。 箭头的粗细表示金额。 这个数字中的分歧可以通过考虑政府和金融市场来解决。
其次,我们介绍了名义GDP(不含进出口)的定义。
- Y = C + G + I = C + T + S
Y是名义GDP,C是从家庭到产品市场的消费支出,G是从政府到产品市场的支出,I是从金融市场到产品市场的投资,T是从家庭到政府的税收,S 是从家庭到金融市场的储蓄。 这里有两个关键词,“从家庭”和“到产品市场”。 常用术语 C 包含这两个关键字。
第三,我们以如下形式引入数量方程。
- MV = PQ
M是通过产品市场的货币总量,V是货币的平均流通速度,P是所有商品和服务的平均价格,Q是所有商品和服务的总量。 该等式显示了两个元素之间的相等性。 一个是一段时间内通过商品和服务市场的货币数量,另一个是在产品市场(=商品和服务市场)上销售的商品和服务。
需要注意的一点是平均分布速度V。你必须正确定义它。 当货币通过商品和服务市场时,这个旋转速度 V 增加 +1,Q 也增加。
包括这篇文章,我不强调“速度”的概念。 1911 年欧文·费雪提出这个公式时,速度的概念在美国似乎是有效的。 这是因为那天住的人多,小店多,理财马虎。 然而,在现代日本,许多人靠月薪生活。 因此,速度是固定的。
2. 三件套一体化
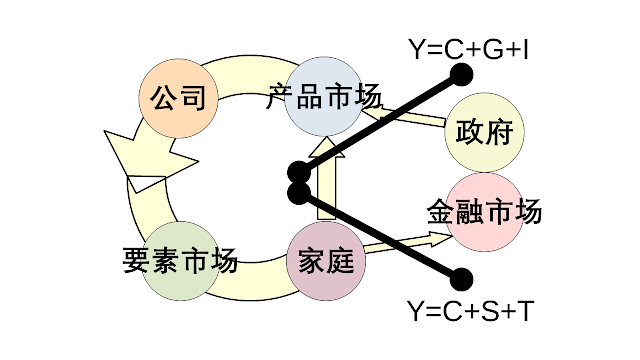
让我们整合我们的三件套。 首先,我们整合了循环流程图和名义GDP的定义。 以下是结果。
为了不矛盾地解释“两件套”,我们假设政府和金融市场在循环流程图之外。 由此可见,一个资金流(T+S)是从家庭到外部(=政府和金融市场),另一个资金流(G+I)是从外部到产品市场。
我们得出结论,GDP的两个不同定义,Y = C+S+T = C+G+I,是对两个不同横截面的货币流动的度量,如上图所示。
接下来,让我们考虑 MV = PQ。 下面的过程是从上述循环流程图解释的货币流通。
- 资金从外部流入产品市场。
- 资金从产品市场流向家庭,然后从家庭流向产品市场。 这个循环重复几次。
- 最后,钱从家庭流向外部。
这导致货币首先作为 G+I 通过产品市场,然后作为 C 通过产品市场。如果货币 G+I 通过产品市场 3 次,我们得到 Y = 3(G+I) = G+ 我+C。 结果,我们从数量方程得到以下关系。
- M=G+I=T+S
- V=Y/(G+I)
我们得出结论,名义 GDP 显示了货币流通中货币的周转次数。 这些关系比货币数量论更合理。
3. 两次资金流动
在这里,让我们考虑两个资金流来简单地解释实际资金流。 这个“二”表示两个货币流通速度,v1 和 v2,并且 v2 = v1+1。 货币数量为 m1 和 m2,那么名义 GDP 表示为,
- 名义 GDP = m1v1 + m2v2。
我们将这个整体除以 G+I = m1+m2。
- 名义GDP / (G+I) = (m1v1 + m2v2) / (m1+m2)
这个方程表明,名义 GDP/(G+I) 是 m1 和 m2 加权后的 v1 和 v2 的平均值。 从名义 GDP/(G+I),我们得到 v1 和 v2。 接下来我们从上述关系中得到 m1 和 m2。
这些价值是货币流通的轮廓。
4. 名义GDP的货币流通
2017年日本名义GDP为546.5万亿日元,家庭消费为295.4万亿日元。 因此,G + I = 250 万亿日元。 在假设有两个资金流的情况下,我们从这些值中得到以下结果。
- 名义GDP / (G + I) = V ~ 2.2
- m1/m2~4
由此,在v1=2的情况下,金额m1为200万亿日元。在v2=3的情况下,金额m2为50万亿日元。
综上所述,2017年日本名义GDP,200万亿日元两次通过产品市场,50万亿日元通过产品市场3次。
这种估计极大地限制了货币流通的现实。 例如,在今天的日本,50 万亿日元不太可能通过产品市场九次。 作者认为这种推导是定量解释货币流通的一个很好的假设。
在过去的 50 年里,货币数量论无法给人们这些价值。 现在我们可以拒绝用 M2 和 M3 对 V 的常规推导。






没有评论:
发表评论