内容。
1. 关系
我们写这篇文章的动机是以下关系。
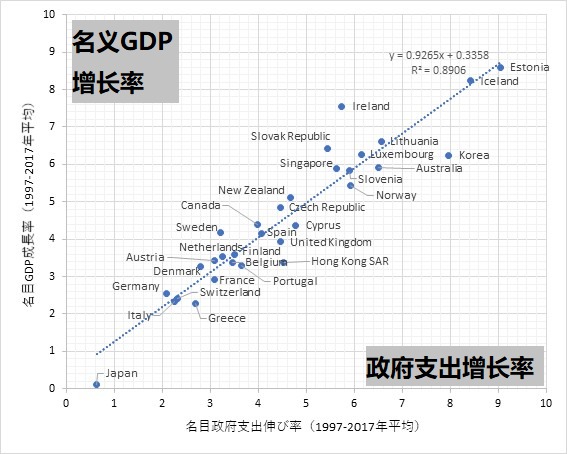
该图显示了名义 GDP 和政府支出之间的增长率关系。 数据来自 31 个国家。 该数据是 20 年的平均值。 这个数字显示了非常令人印象深刻的关系。 名义 GDP 的增长率(y 轴)与政府支出的增长率(x 轴)成正比。 x 轴和 y 轴的范围为 0% 到 10%。
原始图来自以下推文。
以下の散布図の解釈について補足。
— ParkSJ 朴勝俊🌹GND 脱原発!グリーン・ニューディール (@psj95708651) November 8, 2020
長期は生産関数でGDPが決まるなら、仮にY=A×K^β×L^(1-β)【Aは技術、Kは資本、Lは労働】としたとき、小文字をそれぞれの成長率として、
y=a+βk+(1-β)l 【エル】
となる。この式に政府支出の伸び率gは含まれない。従って理論上、yとgの相関はゼロのはず。 pic.twitter.com/oauNRLpFuE
我们不知道这个数字是否包含在已发表的论文中。
2. 我们的推导
这种关系可以描述为,
- dY/Y = dG/G,
其中Y是名义GDP,G是政府支出,dA/A是增长率(=(A2-A1)/A1)。
这种关系可以从数量方程给出。
- Y=MV,
其中 M 是供给货币流通的货币量,V 是货币的流通速度。 这个方程可以变换如下,
- dY/Y = dM/M + dV/V。
这个方程表明名义GDP的增长率是dM/M和dV/V之和。 请注意,这个方程是一个近似方程,可以在这些变化(增长率)大约小于 0.1 时应用。
当 dV/V=0 (dV/V~0) 且 M=aG (`a' 是一个常数值) 时,我们得到观察到的关系。
- dY/Y = dG/G
3. dV/V=0,M=aG
这里,dV/V=0 和 M=aG 来自我们对货币流通的量化观点来看的(“用以了解货币流通的三件套”)。 我们整合了循环流程图、名义 GDP 的定义和数量方程(Fisher 交换方程)来定量理解货币流通。
在这个积分中,我们得到了 M=G+I。 为简化起见,我们设置 M=G+I=aG。 'a' 的值在不同的国家可能不同。
至于dV/V=0,这意味着V的变化远小于M在长时间内的变化。 从我们的定量观点来看,我们得到 V=Y/(G+I)=1/(1-β),其中 β 是平均消费倾向。 我们可以增加政府支出和名义GDP。 但是,每个国家的名义 GDP 中的 β 相对稳定。 如果一个国家发生剧烈变化,β将发生很大变化。






没有评论:
发表评论