在之前的文章《用以了解货币流通的三件套》中,我们解释了货币流通的量化观点。 我们使用了我们的三件套、循环流程图、名义 GDP 的定义和数量方程(Fisher's equation of exchange)。
在本文中,我们介绍了 GDP 定义的整合和数量方程的扩展。 从货币流通的定量观点来看,这些都是合乎逻辑的结果。 本文的内容如下。
1. GDP 定义的整合
我们的结论是,对 GDP 的不同定义是货币流通中不同的横截面。
如上一篇文章所示,通过整合3件套,发现GDP的定义(Y=C+G+I=C+S+T)是指货币流通中的两个横截面。
GDP还有其他定义。 它们被称为生产方面、收入方面和支出方面(=C+G+I)。 这些也是货币流通的横截面。
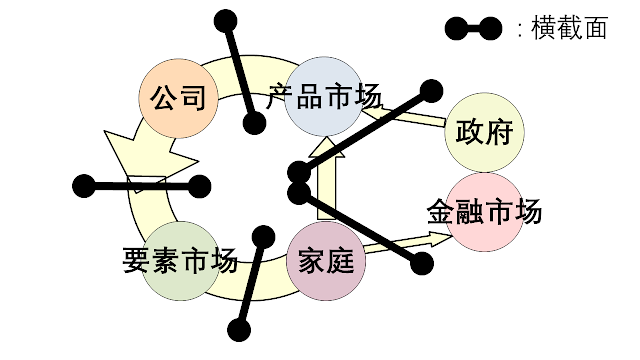
当我们最初发现这种关系时,我们将 GDP 的多个定义与循环流程图进行了比较,以整合我们的三件套。 下图显示了 GDP 定义与循环流程图的关系。
以下将政府和金融市场统称为“外部”。 在上图中,GDP 定义 Y=C+T+S 包括两个横截面。 一种是从家庭到产品市场,一种是从家庭到外部。 另一个 GDP 定义,Y=C+I+G,包括两个横截面。 一种是从家庭到产品市场,一种是从外部到产品市场。
对于 GDP 的其他定义,生产方面是指从产品市场到企业的横截面。 GDP的收入方面是指要素市场对家庭的横截面。
一旦认识到这种融合,这种融合就很自然了。 循环流程图表示货币、商品和服务以及劳动力的流动。 这些流量的大小通过平等联系在一起。 货币流通的不同横截面显示了货币流动的不同方面。
2. 数量方程的扩展
我们的结论是,通过对 GDP 定义的整合,我们可以扩展数量方程。
原始数量方程(Fisher 交换方程)为 MV=PQ。 这个 MV 表示通过产品市场的总金额。 PQ 表示企业销售的产品总量。 鉴于一年的测量期,这些金额是名义 GDP。
根据 GDP 定义的整合,可以将货币流动的其他方面与数量方程联系起来。 我们建议扩展数量方程,如下所示。
 |
| 数量方程的扩展。 |
这里,NO 是所有家庭的总收入。 N'PS 是所有消费者消费和接受的商品和服务的总量。 在这些产品中,N 是家庭总数,O 是平均收入,N' 是消费者总数,P 是平均价格,S 是一个消费者消费和接受的商品和服务的总数。
人们很容易接受家庭的总收入,NO。 这是因为它是 GDP 的收入方面。 其次,N'PS 是消费者消费和接受的商品和服务的总量。 请注意,这里的“接受商品和服务”是指不需要直接支付金钱的公共服务。 例如,这些是公共教育、和平与秩序、对外外交、科学进步等。
这个 N' 不是家庭总数,而是消费者总数。 因此,这个 N' 等于总体。 这里采用消费者总数,我们可以通过 NO=N'PS 来讨论一个工人(家庭)对一个消费者的商品和服务总数的生产能力。
我们不能向读者保证,我们对数量方程的扩展可以涵盖整个货币流通。 这是一个悬而未决的问题。






没有评论:
发表评论